The evolution of local 3D tissue compressibility in the heart wall may be a sensitive indicator of myocardial perfusion. Characterizing the compressibility of the myocardial tissue in the intact heart is also crucial for the accurate prediction of wall stresses using finite element analysis[1].
THEORY:
Magnetic Resonance (MR) imaging with cardiac tagging has been used to track
myocardial material points throughout the left ventricle (LV)
with estimated <0.3mm accuracy[2]. Following a displacement field-fitting
reconstruction, the
gradient of the 3D displacement field is used to compute the deformation
gradient tensor, F, at any point in the heart wall. The determinant of
F gives a measure of the
local change in volume, or compressibility,
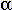. The compressibility
of myocardial tissue is expected to vary as much as 5--10% over the cardiac
cycle due to pulsatile coronary flow and heterogenous stress distributions in
the heart wall.
METHODS:
Computer models of a deforming prolate spheroid, based on strain patterns
measured in a beating heart, were used to simulate a low and a high density
tagged image data sets[2]. The low tag density set corresponded to
the number of
short and long axis slices (6-7) and tag separation (6-7mm) used for clinical
investigation. The high density set matches the tag density used for cardiac
mechanics research. Field-fits were performed optimially for each
data density. The deformation model has material compressibility values that
range from 0.85 to one.
An isolated, arrested, non-perfused experimental canine heart model undergoing passive inflation was used to verify the technique in a deforming heart where the tissue is expected to be nearly incompressible.
To investigate the effect of noise in the raw tag displacement data on a noiseless data set with a physiologic geometry and deformation field, a Monte Carlo simulation was performed on a reconstructed isolated heart.
The compressibility error over all the material mesh points for the low density mathematical heart model was -0.02 +/- 0.118, while that for the high density tag set was -0.01 +/- 0.02. The error was smallest toward the midwall and away from the most basal and most apical levels.
For the isolated canine heart, the percent of myocardial volume which had
an 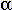within a set of prescribed ranges was
computed for each of three transmural regions in the LV wall, shown in Table 1.
The estimated compressibility was closest to the expected value toward the
midwall, with 79% of the midwall volume having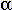
fall within 2% of that expected. The endocardial region had the largest error,
with ~60% of the volume within 2% of the expected value.
| Wall Depth | ||||
|---|---|---|---|---|
| 0 to 4mm | 4--8mm | 8--endo | ||
|
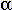
R a n g e |
0.85-1.15 | 100 | 100 | 99.9 |
| 0.90-1.10 | 100 | 99.7 | 98.7 | |
| 0.95-1.05 | 94.9 | 95.2 | 89.1 | |
| 0.98-1.02 | 68.1 | 79.0 | 60.4 | |
| 0.99-1.01 | 47.6 | 58.9 | 39.3 | |
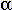within each prescribed range. The wall has
been subdivided into three transmural regions.
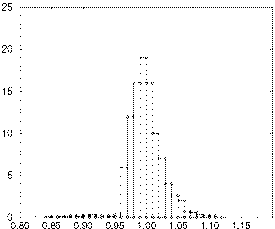
For the midwall region, a histogram of the percent wall volume versus
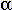is shown in Figure 1. The mean of this
distribution is 1.0, with a standard deviation of 0.026.
For an input noise standard deviation of 0.25mm (larger than the expected uncertainty of <0.1mm[3]) and 50 Monte Carlo runs, the error in the estimated compressibility due to noise alone was 0.012 with a spread (SD) of 0.025.
 |
 |
|---|---|
| Compressibility |
DISCUSSION:
For the range of compressibilites expected in the intact and beating heart, the
typical tagging and imaging density used for clinical investigation is not
adequate for compressibility analysis using the present reconstruction
technique. However, for the density used typically for
research, the technique is accurate, with an expected SD error < 2%. The
spread can be attributed largely to reconstruction error (found to be 2% for
a 3D mathematical deformation model) and to the propagation of noise in the tag
displacement data (with an upper bound of 0.025 determined from a Monte Carlo
simulation on a reconstructed real-heart data set). These numbers agree well
with the results from an isolated heart model where the compressibility at
a midwall shell was found to be 1.0 (the expected value) with a spread of
0.026 (or 2.6% SD error).
This analysis validates the method of computing compressibility in the intact
heart using MR tagging and displacement field-fitting reconstruction.
These findings also support the use of an assumption of tissue incompressibility
for finite element modeling of non-perfused, passively deforming canine hearts.
References:
1. McCulloch A, Guccione J, Waldman L and Rogers J,
High-Performance Computing in Biomedical Research,
CRC Press, Boca Raton, 1993.
2. O'Dell WG, Moore CC, Hunter WC, Zerhouni EA and McVeigh ER,
Radiology, June; p 829-835, 1995.
3. McVeigh ER and Atalar E Magn. Reson. Med., 28, 318-327, 1992.